Fisher.Understanding
Reading: Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 6 and Chapter 4
Synopsis: In this article we finish up the Fisher paper by looking at a couple of leftover topics. As you read through the article, try and draw the Lee diagrams before looking at the graphs as this will help you understand the process better.
Study Tips
Read this article first and then skim the source text.
Estimated study time: 1 Hour (not including subsequent review time)
BattleTable
Based on past exams, the main things you need to know (in rough order of importance) are:
- fact A...
- fact B...
reference part (a) part (b) part (c) part (d) E (2018.Spring #1) E (2018.Spring #1) E (2018.Spring #1) E (2018.Spring #1) E (2018.Spring #1) E (2018.Spring #1) E (2018.Spring #1) E (2018.Spring #1)
In Plain English!
Understanding Aggregate Loss Distributions
In general, for two risks with the same expected loss, the smaller risk has more variability than a large risk that has a high number of less severe claims.
The distribution of entry ratios (the r values) is mainly shaped by the variance of the severity distribution. However, the distribution of insurance charges (the [math]\phi(r)[/math] values) is driven more by the variance of the claim frequency distribution. To see this it's helpful to consider two extreme cases.
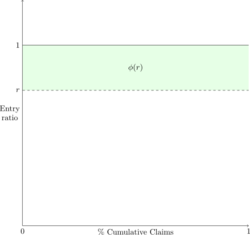
Case 1: Suppose we have a large number of policies, all of which experience exactly one loss of $100. The expected loss is also $100. The entry ratio is the actual loss divided by the expected loss, so in this case all policies have the same entry ratio of 1.000. This allows us to draw the following Lee diagram (see Figure 1). From Figure 1 we see [math]\phi(r) = \begin{cases} 0 &\mbox{if } r\ge 1\\ 1-r & \mbox{if }0\le r \lt 1 \end{cases}[/math]. We observe both the severity distribution and distribution of entry ratios have no variance.
Case 2: Suppose we have 10,000 policies where 9,999 experience no loss, and one has a loss of $1 million. The expected loss is $100 and the entry ratios are 0 for 9,999 policies and then 10,000 for the last policy. This scenario has the following Lee diagram (see Figure 2).
The blue line in Figure 2 shows the entry ratio, it is zero from the origin to 0.9999 and then jumps to 10,000 at 1.000. Since the data is discrete, the blue vertical line is really a rectangle of width 1/10,000. Hence we compute the insurance charge as [math]\phi(r) =\frac{10,000 - r}{10,000}=1-\frac{r}{10,000}[/math]. We observe the variance of the severity distribution and the variance of the entry ratios have increased.
Case 1 is an extreme example of the type of behaviour expected from a large commercial policy having lots of similar and highly predictable claims. Case 2 is an extreme example of a very small policy, where a claim is unlikely to occur but if it does then it is likely in the (right) tail of the severity distribution.
Key Points:
- The larger the number of expected claims, the smaller the entry ratio variance is and the lower the insurance charge is for entry ratios greater than 1.
- Similarly, the entry ratio variance increases as the likelihood of a loss for away from the expected severity increases.
- Most of the aggregate loss variance is driven by the size of the policy, i.e. driven by the claim frequency variance. However, Fisher's next example shows the severity distribution variance contributes as well.
Case 3: Suppose there are two types of policy, A and B, both of which have an expected claim frequency of 1 and no variance (i.e. always have 1 claim). Further, let Policy A have a 50% change of a $1,000 loss or $5,000 loss, and let Policy B have a 60% chance of a $500 loss, 30% chance of a $5,000 loss, and a 10% chance of a $12,000 loss. Policies A and B both have the same expected value of $3,000, but Var(A) = 1,500 and Var(B) = 3,612.48.
Using a representative sample of 10 policies of each type, we can draw the pair of Lee diagrams seen in Figure 3. By calculating each of the green shaded areas we see the insurance charge at entry ratio 1 is 0.5 for Policy B, whereas for Policy A it is 0.333. The severity distribution for Policy B has greater variance than the severity distribution for Policy A, and we note there are no differences between the policies in terms of claim frequency.
To reflect these differences in practice, the NCCI assigns workers' compensation jobs into seven hazard groups (see Robertson.HazardGroups). Group A has the lowest probability of a serious injury leading to an unusually high claim severity, whereas Group G has the highest probability of a serious injury leading to an unusually high claim severity.
Since workers' compensation laws plus the cost and level of care available vary by state, the NCCI Table M has an adjustment factor to account for the variation between states and hazard groups (see NCCI.ExperienceRating).