Fisher.LimitedTableM: Difference between revisions
| (21 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
'''Reading''': Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 4 | '''Reading''': Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 4 | ||
'''Synopsis''': This is a quick read but you must pay close attention to how the losses are limited due to the interaction between a per-occurrence deductible and an aggregate deductible limit. | '''Synopsis''': This is a quick read but you must pay close attention to how the losses are limited due to the interaction between a per-occurrence deductible and an aggregate deductible/limit. | ||
==Study Tips== | ==Study Tips== | ||
.. | Perhaps the hardest part of this reading is getting used to allocating the losses between the per-occurrence excess and the aggregate excess. You need to get really good at that so you can focus on the broader question. You should also know how to apply the retrospective rating formula when there is a per-occurrence deductible and an aggregate deductible. | ||
'''Estimated study time''': | '''Estimated study time''': 8 Hours ''(not including subsequent review time)'' | ||
==BattleTable== | ==BattleTable== | ||
| Line 13: | Line 13: | ||
Based on past exams, the '''main things''' you need to know ''(in rough order of importance)'' are: | Based on past exams, the '''main things''' you need to know ''(in rough order of importance)'' are: | ||
* | * How to allocate actual losses between the per-occurrence excess and aggregate excess. | ||
* | * How to use the allocated losses to build a Limited Table M using either the vertical or horizontal slices method. | ||
* How to use a Limited Table M to calculate the total loss cost for a policy with both a per-occurrence deductible and an aggregate excess deductible. | |||
: {| class='wikitable' style='width: 1000px;' | : {| class='wikitable' style='width: 1000px;' | ||
| Line 22: | Line 23: | ||
|- | |- | ||
|| no | || <span style="color:red;">'''Currently no exam questions for this reading'''</span> | ||
|| | | style="background-color: lightgrey;"| | ||
|| | | style="background-color: lightgrey;"| | ||
|| | | style="background-color: lightgrey;"| | ||
|| | | style="background-color: lightgrey;"| | ||
|} | |} | ||
<!-- ******** BattleBar Code ******** --> | |||
{|style="border: solid; color:lightgrey; border-radius:10px; border-width:2px; align:center;" | |||
|- | |||
<!-- ******** Full BattleQuiz ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=LimitedTableM§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''Full BattleQuiz]'''</span> | |||
<!-- --> | |||
<!-- ******** Excel BattleQuiz ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=LimitedTableM§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="color: red; font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; border-color: darkblue; padding: 2px 10px 2px 10px; margin: 0px;">'''''Excel BattleQuiz]'''''</span> | |||
--> | |||
<!-- --> | |||
<!-- ******** Excel PowerPack Files ******** --> | |||
|style="padding:2px"|[[BattleActs_PowerPack#ppFisher| <span style="color: white; font-size: 12px; background-color: indigo; border: solid; border-width: 2px; border-radius: 10px; border-color: indigo; padding: 1px 3px 1px 3px; margin: 0px;">'''''Excel Files '''''</span>]] | |||
<!-- --> | |||
<!-- ******** Forum ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/index.php?p=/categories/fisher-limitedtablem<span style="font-size: 12px; background-color: lightgrey; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Forum'''</span>] | |||
<!-- --> | |||
<!-- ******** Formula Sheet ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/categories/fisher-limitedtablem<span style="font-size: 12px; color: darkblue; background-color: lightblue; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Formula Sheet'''</span>] | |||
--> | |||
|} | |||
<span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | |||
==In Plain English!== | ==In Plain English!== | ||
In [[Fisher.TableM]] we learned how to create a Table M to estimate aggregate loss costs without a per-claim limit. However, in reality most policies have a per-occurrence limit (or deductible) <u>and</u> an aggregate limit which caps the insured's maximum out of pocket. For instance, a policy may have a per-occurrence limit of $100,000 which means the insured is responsible for the first $100,000 of any claim. The same policy may also have an aggregate limit of $250,000. This means once the insured has been responsible for claims where the portion under $100,000 totals at least $250,000 then they are only responsible for $250,000 so the insured is no longer responsible for paying any part of claims. | In ''[[Fisher.TableM]]'' we learned how to create a Table M to estimate aggregate loss costs without a per-claim limit. However, in reality most policies have a per-occurrence limit (or deductible) <u>and</u> an aggregate limit which caps the insured's maximum out of pocket. For instance, a policy may have a per-occurrence limit of $100,000 which means the insured is responsible for the first $100,000 of any claim. The same policy may also have an aggregate limit of $250,000. This means once the insured has been responsible for claims where the portion under $100,000 totals at least $250,000 then they are only responsible for $250,000 so the insured is no longer responsible for paying any part of claims. | ||
The per-occurrence limit reduces the variance of the aggregate loss distribution by reducing the variance of the severity distribution. | The per-occurrence limit reduces the variance of the aggregate loss distribution by reducing the variance of the severity distribution. | ||
| Line 38: | Line 63: | ||
# Separately price losses in excess of the per-occurrence limit (deductible), ''D'', and then price for losses in excess of the aggregate limit. | # Separately price losses in excess of the per-occurrence limit (deductible), ''D'', and then price for losses in excess of the aggregate limit. | ||
#*This is the <span style="color:red;">'''Limited Table M'''</span> approach that we'll discuss here. | #*This is the <span style="color:red;">'''Limited Table M'''</span> approach that we'll discuss here. | ||
# Price it all at once - this is the California Table L approach (see [[Fisher.TableL]]) | # Price it all at once - this is the California Table L approach (see ''[[Fisher.TableL]]'') | ||
:{| class="wikitable" | :{| class="wikitable" | ||
|- | |- | ||
|'''Question:''' What are two reasons it may be preferable to price separately using approach 1? | |'''Question:''' What are two reasons why it may be preferable to price separately using approach 1? | ||
|} | |} | ||
:<span style="color: | :<span style="color:purple;">'''Solution:'''</span> | ||
* There may be enough data to update the per-occurrence excess charge | :* There may be enough data to update the per-occurrence excess charge more often than the aggregate excess charge. | ||
* It may be possible to use two different data sources for the calculations. | :* It may be possible to use two different data sources for the calculations. Both the NCCI and ISO retrospective rating plans use different data sources. | ||
<u>'''Key Issue:'''</u> | <u>'''Key Issue:'''</u> | ||
| Line 62: | Line 87: | ||
|} | |} | ||
:<span style="color: | :<span style="color:purple";>'''Solution:'''</span> | ||
:{|class="wikitable" | :{|class="wikitable" | ||
|- | |- | ||
| Line 81: | Line 106: | ||
: When pricing the excess charge for the aggregate limit you must use the limited amounts in the "restricted by per-occurrence limit" column. That is, the aggregate limit is priced using losses in the primary layer (the "limited layer"). | : When pricing the excess charge for the aggregate limit you must use the limited amounts in the "restricted by per-occurrence limit" column. That is, the aggregate limit is priced using losses in the primary layer (the "limited layer"). | ||
Once the losses have been correctly adjusted for the per-occurrence limit, you can use either of the vertical or horizontal slicing methods to develop the Limited Table M in the same way as we did in [[Fisher.TableM]]. The key difference is the entry ratio which, for a Limited Table M, is defined as <math>r=\frac{\mbox{actual limited aggregate loss}}{\mbox{expected limited aggregate loss}}=\frac{A_D}{E[A_D]}</math>. | Once the losses have been correctly adjusted for the per-occurrence limit, you can use either of the vertical or horizontal slicing methods to develop the Limited Table M in the same way as we did in ''[[Fisher.TableM]]''. The key difference is the entry ratio which, for a Limited Table M, is defined as <math>r=\frac{\mbox{actual limited aggregate loss}}{\mbox{expected limited aggregate loss}}=\frac{A_D}{E[A_D]}</math>. | ||
Let's look at an application of a Limited Table M from the text. | Let's look at an application of a Limited Table M from the text. | ||
| Line 89: | Line 114: | ||
|} | |} | ||
:<span style="color: | :<span style="color:purple;">'''Solution:'''</span> | ||
:First calculate the entry ratio which is <math>r=\frac{A_D}{E[A_D]}=\frac{1,000,000}{800,000}=1.25</math>. Next, look up the insurance charge for this entry ratio in the Limited Table M with deductible <math>D=250,000</math>. Suppose we find <math>\phi(1.25)=0.18</math> then the loss cost for the aggregate deductible limit is <math>\phi(r)\cdot E[A_D]=0.18\cdot 800,000=$144,000</math>. | :First calculate the entry ratio which is <math>r=\frac{A_D}{E[A_D]}=\frac{1,\!000,\!000}{800,\!000}=1.25</math>. Next, look up the insurance charge for this entry ratio in the Limited Table M with deductible <math>D=250,\!000</math>. Suppose we find <math>\phi(1.25)=0.18</math> then the loss cost for the aggregate deductible limit is <math>\phi(r)\cdot E[A_D]=0.18\cdot 800,\!000=$144,\!000</math>. | ||
:<u>Note:</u> This is not the loss cost for the policy because we assume the per-occurrence deductible is priced separately. The per-occurrence loss cost needs to be added on to the loss cost of the aggregate deductible to get the total loss cost for the policy. | :<u>Note:</u> This is not the loss cost for the policy because we assume the per-occurrence deductible is priced separately. The per-occurrence loss cost needs to be added on to the loss cost of the aggregate deductible to get the total loss cost for the policy. | ||
| Line 116: | Line 141: | ||
|} | |} | ||
:<span style="color: | :<span style="color:purple;">'''Solution:'''</span> | ||
:We're given the entry ratio and deductible so we find <math>\phi(2.0)=0.040</math>. We also know the loss cost for the aggregate deductible limit is <math>\phi(r)\cdot E[A_D]=0.040\cdot (500,000)=$20,000</math>. Here we're recalling primary losses are those below the per-occurrence deductible. Lastly, we need the expected loss cost for losses in excess of the per-occurrence deductible. This is given by <math>E-E[A_D]=700,000-500,000 = $200,000</math>. | :We're given the entry ratio and deductible so we find <math>\phi(2.0)=0.040</math>. We also know the loss cost for the aggregate deductible limit is <math>\phi(r)\cdot E[A_D]=0.040\cdot (500,\!000)=$20,\!000</math>. Here we're recalling primary losses are those below the per-occurrence deductible. Lastly, we need the expected loss cost for losses in excess of the per-occurrence deductible. This is given by <math>E-E[A_D]=700,\!000-500,\!000 = $200,\!000</math>. | ||
:So the total expected loss cost for the policy is <math>20,000+200,000 = $220,000</math>. | :So the total expected loss cost for the policy is <math>20,\!000 + 200,\!000 = $220,\!000</math>. | ||
Now let's try a slightly more involved example. | Now let's try a slightly more involved example. | ||
| Line 128: | Line 153: | ||
|} | |} | ||
:<span style="color: | :<span style="color:purple;">'''Solution:'''</span> | ||
:First we need the entry ratio which is <math>r=\frac{A_D}{E[A_D]}=\frac{1,\!000,\!000}{400,\!000}=2.5</math>. Next, although we have the entry ratio in the Limited Table M, we do not have a column for the $150,000 deductible so we need to interpolate between the insurance charge factors for the 100k and 250k deductibles at entry ratio 2.5. This yields the insurance charge as <math>\phi(2.5)=\frac{1}{3}\cdot 0.022 + \frac{2}{3}\cdot0.018 = 0.0193</math>. | |||
:Using this we get the aggregate limit loss cost is <math>\phi(2.5)\cdot E[A_D]=0.0193\cdot 400,\!000=\$7,\!733.33.</math> | |||
:Lastly, the loss cost for the per-occurrence excess is <math>E[A]-E[A_D]=700,\!000-400,\!000=$300,\!000.</math> So the total loss cost for the policy is <math>7,\!733.33+300,\!000= \$307,\!733.33.</math> | |||
Here's an example from the text of how the CAS could test this material: | |||
: <span class="newwin">[https://www.battleacts8.ca/8/pdf/Fisher_Ch3Q13.pdf <span style="color: white; font-size: 12px; background-color: green; border: solid; border-width: 2px; border-radius: 10px; border-color: green; padding: 1px 3px 1px 3px; margin: 0px;">'''''Calculating the cost of per-occurrence and aggregate deductibles'''''</span>]</span> | |||
===Calculating Retrospective Premiums=== | |||
We can use the retrospective rating formula <math>R=(B+cL)T</math> when a policy has both a per-occurrence deductible and an aggregate deductible. Here's an example: | |||
:{| class="wikitable" | |||
|- | |||
||'''Question:'''||Calculate the retrospective premium given the following policy and loss information. | |||
|- | |||
||$40,000||Basic Premium | |||
|- | |||
||$15,000||Excess Premium | |||
|- | |||
||1.09||Loss Conversion Factor | |||
|- | |||
||4%||Tax Rate | |||
|- | |||
||$90,000||Per-occurrence limit | |||
|- | |||
||$260,000||Maximum Premium | |||
|- | |||
||$140,000||Total loss, consists of 0 losses over $90,000 | |||
|} | |||
:<span style="color:purple;">'''Solution'''</span> | |||
:First add the basic and excess premiums together to get the initial premium, ''B'' = $55,000. Next, determine the ratable loss, ''L'', by assessing if there are any large losses as these would contribute the per-occurrence limit, then add on the "small losses" before finally considering if there are any maximum or minimum ratable loss restrictions. Here we get ''L'' = $140,000 as there are no large losses. Now we apply the retrospective rating formula to get <math>R=(55,\!000 + 1.09\cdot 140,\!000)\cdot 1/(1-4\%)=\$216,\!250.</math> | |||
: | There are a couple of different situations that can arise, such as the ratable loss being large enough to cause the retrospective premium to be capped by the maximum premium. This could happen due to: | ||
# There being sufficiently many small losses to make ''L'' "too large". In this case the insured is said to <u>benefit from the maximum premium</u>, or | |||
# There may be a large loss and no other losses, in which case the insured <u>benefits from the per-occurrence limit</u>, or | |||
# A combination of both of the above may occur, or the capped large loss plus the small losses still results in a loss amount over the maximum ratable loss. In this case, although the insured was able to cap the large loss, it didn't change their retrospective premium. This would be an example of the <u>overlap between the maximum premium and accident limit</u>. | |||
Similar situations can arise when there is a minimum premium. The <u>underlap between the minimum premium and accident limit</u> occurs when there is no benefit from the accident limit even when there is a large loss because the minimum premium is sufficiently high. | |||
: | Just work through the logic carefully as you solve problems - all you really need is the retrospective rating formula. | ||
<!-- | |||
Here's another example of how the CAS could test this topic. | |||
: <span class="newwin">[https://www.battleacts8.ca/8/pdf/Fisher_Ch3Q12.pdf <span style="color: white; font-size: 12px; background-color: green; border: solid; border-width: 2px; border-radius: 10px; border-color: green; padding: 1px 3px 1px 3px; margin: 0px;">'''''Combining the per-occurrence and excess charges'''''</span>]</span> | |||
--> | |||
===Limited Table M & Lee Diagrams=== | |||
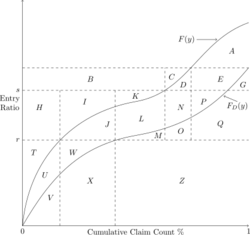
The relationships found in ''[[Fisher.Visualization]]'' and ''[[Fisher.TableM]]'' apply when calculating with a Limited Table M. Figure 1 below shows the unlimited aggregate loss curve ''F(y)'' and the aggregate loss curve limited by the per-occurrence deductible (D), ''F<sub>D</sub>(y)''. The Limited Table M (Table M<sub>D</sub>) charge at entry ratio ''s'' is the area denoted by ''G''. The Limited Table M savings at entry ratio ''r'' is the area denoted by T + U + W. The per-occurrence excess charge is the area between the two curves, that is A + E + D + P + N + L + J + W + U. | |||
[[File:LimitedTableMFig1.png|thumb|250px|center|Figure 1]] | |||
===Closing Remarks=== | ===Closing Remarks=== | ||
The size of the per-occurrence limit (deductible) heavily influences the distribution of primary losses. This means a Limited Table M must be calculated for each deductible offered. Usually the unlimited losses (i.e. losses before applying a per-occurrence or aggregate limit) are known which makes it straight forward to adjust the losses to the required deductible. | The size of the per-occurrence limit (deductible) heavily influences the distribution of primary losses. This means a Limited Table M must be calculated for each deductible offered. Usually the unlimited losses (i.e. losses before applying a per-occurrence or aggregate limit) are known which makes it straight forward to adjust the losses to the required deductible. | ||
Loss distributions are usually positively skewed so have many small losses and few large losses. This means the variance of the loss distribution is mostly determined by the larger losses. As we lower the per-occurrence limit the severity distribution variance decreases as frequency is unchanged. This reduces the likelihood of larger limited aggregate losses so lower deductibles normally result in lower insurance charges for entry ratios greater than 1. | Loss distributions are usually positively skewed so have many small losses and few large losses. This means the variance of the loss distribution is mostly determined by the larger losses. As we lower the per-occurrence limit the severity distribution variance decreases as frequency is unchanged. This reduces the likelihood of larger limited aggregate losses so lower deductibles normally result in lower insurance charges for entry ratios greater than 1. | ||
== | <!-- ******** BattleBar Code ******** --> | ||
{|style="border: solid; color:lightgrey; border-radius:10px; border-width:2px; align:center;" | |||
|- | |||
<!-- ******** Full BattleQuiz ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=LimitedTableM§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''Full BattleQuiz]'''</span> | |||
<!-- --> | |||
<!-- ******** Excel BattleQuiz ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=LimitedTableM§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="color: red; font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; border-color: darkblue; padding: 2px 10px 2px 10px; margin: 0px;">'''''Excel BattleQuiz]'''''</span> | |||
--> | |||
<!-- --> | |||
<!-- ******** Excel PowerPack Files ******** --> | |||
|style="padding:2px"|[[BattleActs_PowerPack#ppFisher| <span style="color: white; font-size: 12px; background-color: indigo; border: solid; border-width: 2px; border-radius: 10px; border-color: indigo; padding: 1px 3px 1px 3px; margin: 0px;">'''''Excel Files '''''</span>]] | |||
<!-- --> | |||
<!-- ******** Forum ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/index.php?p=/categories/fisher-limitedtablem<span style="font-size: 12px; background-color: lightgrey; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Forum'''</span>] | |||
<!-- --> | |||
<!-- ******** Formula Sheet ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/categories/fisher-limitedtablem<span style="font-size: 12px; color: darkblue; background-color: lightblue; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Formula Sheet'''</span>] | |||
--> | |||
|} | |||
<span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | |||
Latest revision as of 10:54, 14 July 2024
Reading: Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 4
Synopsis: This is a quick read but you must pay close attention to how the losses are limited due to the interaction between a per-occurrence deductible and an aggregate deductible/limit.
Study Tips
Perhaps the hardest part of this reading is getting used to allocating the losses between the per-occurrence excess and the aggregate excess. You need to get really good at that so you can focus on the broader question. You should also know how to apply the retrospective rating formula when there is a per-occurrence deductible and an aggregate deductible.
Estimated study time: 8 Hours (not including subsequent review time)
BattleTable
Based on past exams, the main things you need to know (in rough order of importance) are:
- How to allocate actual losses between the per-occurrence excess and aggregate excess.
- How to use the allocated losses to build a Limited Table M using either the vertical or horizontal slices method.
- How to use a Limited Table M to calculate the total loss cost for a policy with both a per-occurrence deductible and an aggregate excess deductible.
reference part (a) part (b) part (c) part (d) Currently no exam questions for this reading
| Full BattleQuiz | Excel Files | Forum |
You must be logged in or this will not work.
In Plain English!
In Fisher.TableM we learned how to create a Table M to estimate aggregate loss costs without a per-claim limit. However, in reality most policies have a per-occurrence limit (or deductible) and an aggregate limit which caps the insured's maximum out of pocket. For instance, a policy may have a per-occurrence limit of $100,000 which means the insured is responsible for the first $100,000 of any claim. The same policy may also have an aggregate limit of $250,000. This means once the insured has been responsible for claims where the portion under $100,000 totals at least $250,000 then they are only responsible for $250,000 so the insured is no longer responsible for paying any part of claims.
The per-occurrence limit reduces the variance of the aggregate loss distribution by reducing the variance of the severity distribution.
There are two possible approaches for pricing such a policy.
- Separately price losses in excess of the per-occurrence limit (deductible), D, and then price for losses in excess of the aggregate limit.
- This is the Limited Table M approach that we'll discuss here.
- Price it all at once - this is the California Table L approach (see Fisher.TableL)
Question: What are two reasons why it may be preferable to price separately using approach 1?
- Solution:
- There may be enough data to update the per-occurrence excess charge more often than the aggregate excess charge.
- It may be possible to use two different data sources for the calculations. Both the NCCI and ISO retrospective rating plans use different data sources.
Key Issue: Consider a policy with a per-occurrence limit of $100,000 and an aggregate limit of $250,000. Suppose a claim has come in for $275,000. This claim is $175,000 over the per-occurrence limit, but also $25,000 over the aggregate limit without even taking into account if there are any prior claims. How much of the loss is applied to each limit?
In this situation it is usual to apply the per-occurrence limit first, so $175,000 is excess of the per-occurrence limit. We count the difference, namely $100,000, towards the aggregate limit. This avoids double counting of losses.
For the remainder of this article, assume the per-occurrence excess charge is known and was calculated using losses that were not subject to an aggregate limit. Then before pricing the aggregate limit, it is important to restrict all losses by the per-occurrence limit.
Question: A policy has a $100,000 per-occurrence limit and an aggregate limit of $250,000. It experiences the following unlimited claims: $60,000; $70,000; $90,000; $110,000; $120,000.
What are the claim amounts that should be used for pricing the aggregate limit?
- Solution:
Claim Number Unlimited Amount Restricted by per-occurrence limit 1 $60,000 $60,000 2 $70,000 $70,000 3 $90,000 $90,000 4 $110,000 $100,000 5 $120,000 $100,000 Total $450,000 $420,000
- When pricing the excess charge for the aggregate limit you must use the limited amounts in the "restricted by per-occurrence limit" column. That is, the aggregate limit is priced using losses in the primary layer (the "limited layer").
Once the losses have been correctly adjusted for the per-occurrence limit, you can use either of the vertical or horizontal slicing methods to develop the Limited Table M in the same way as we did in Fisher.TableM. The key difference is the entry ratio which, for a Limited Table M, is defined as [math]r=\frac{\mbox{actual limited aggregate loss}}{\mbox{expected limited aggregate loss}}=\frac{A_D}{E[A_D]}[/math].
Let's look at an application of a Limited Table M from the text.
Question: A workers' compensation policy has a per-occurrence deductible of $250,000, has expected limited aggregate losses of $800,000, and has an aggregate deductible limit of $1,000,000. Calculate the loss cost for the aggregate deductible limit.
- Solution:
- First calculate the entry ratio which is [math]r=\frac{A_D}{E[A_D]}=\frac{1,\!000,\!000}{800,\!000}=1.25[/math]. Next, look up the insurance charge for this entry ratio in the Limited Table M with deductible [math]D=250,\!000[/math]. Suppose we find [math]\phi(1.25)=0.18[/math] then the loss cost for the aggregate deductible limit is [math]\phi(r)\cdot E[A_D]=0.18\cdot 800,\!000=$144,\!000[/math].
- Note: This is not the loss cost for the policy because we assume the per-occurrence deductible is priced separately. The per-occurrence loss cost needs to be added on to the loss cost of the aggregate deductible to get the total loss cost for the policy.
The following example ties this all together.
Question: A workers' compensation policy has expected total losses of $700,000 along with a $250,000 per-occurrence deductible, expected primary losses of $500,000 and an entry ratio of 2.0. Calculate the total expected loss cost for the policy given the Limited Table M below.
Insurance Charge Factor Deductible Entry Ratio $100,000 $250,000 $500,000 1.0 0.240 0.250 0.260 1.5 0.100 0.110 0.120 2.0 0.030 0.040 0.050 2.5 0.018 0.022 0.030
- Solution:
- We're given the entry ratio and deductible so we find [math]\phi(2.0)=0.040[/math]. We also know the loss cost for the aggregate deductible limit is [math]\phi(r)\cdot E[A_D]=0.040\cdot (500,\!000)=$20,\!000[/math]. Here we're recalling primary losses are those below the per-occurrence deductible. Lastly, we need the expected loss cost for losses in excess of the per-occurrence deductible. This is given by [math]E-E[A_D]=700,\!000-500,\!000 = $200,\!000[/math].
- So the total expected loss cost for the policy is [math]20,\!000 + 200,\!000 = $220,\!000[/math].
Now let's try a slightly more involved example.
Question: Suppose the policy has expected total losses = $700,000, expected primary losses = $400,000, a per-occurrence deductible of $150,000, and an aggregate limit of $1,000,000. Calculate the total expected loss cost for the policy.
- Solution:
- First we need the entry ratio which is [math]r=\frac{A_D}{E[A_D]}=\frac{1,\!000,\!000}{400,\!000}=2.5[/math]. Next, although we have the entry ratio in the Limited Table M, we do not have a column for the $150,000 deductible so we need to interpolate between the insurance charge factors for the 100k and 250k deductibles at entry ratio 2.5. This yields the insurance charge as [math]\phi(2.5)=\frac{1}{3}\cdot 0.022 + \frac{2}{3}\cdot0.018 = 0.0193[/math].
- Using this we get the aggregate limit loss cost is [math]\phi(2.5)\cdot E[A_D]=0.0193\cdot 400,\!000=\$7,\!733.33.[/math]
- Lastly, the loss cost for the per-occurrence excess is [math]E[A]-E[A_D]=700,\!000-400,\!000=$300,\!000.[/math] So the total loss cost for the policy is [math]7,\!733.33+300,\!000= \$307,\!733.33.[/math]
Here's an example from the text of how the CAS could test this material:
Calculating Retrospective Premiums
We can use the retrospective rating formula [math]R=(B+cL)T[/math] when a policy has both a per-occurrence deductible and an aggregate deductible. Here's an example:
Question: Calculate the retrospective premium given the following policy and loss information. $40,000 Basic Premium $15,000 Excess Premium 1.09 Loss Conversion Factor 4% Tax Rate $90,000 Per-occurrence limit $260,000 Maximum Premium $140,000 Total loss, consists of 0 losses over $90,000
- Solution
- First add the basic and excess premiums together to get the initial premium, B = $55,000. Next, determine the ratable loss, L, by assessing if there are any large losses as these would contribute the per-occurrence limit, then add on the "small losses" before finally considering if there are any maximum or minimum ratable loss restrictions. Here we get L = $140,000 as there are no large losses. Now we apply the retrospective rating formula to get [math]R=(55,\!000 + 1.09\cdot 140,\!000)\cdot 1/(1-4\%)=\$216,\!250.[/math]
There are a couple of different situations that can arise, such as the ratable loss being large enough to cause the retrospective premium to be capped by the maximum premium. This could happen due to:
- There being sufficiently many small losses to make L "too large". In this case the insured is said to benefit from the maximum premium, or
- There may be a large loss and no other losses, in which case the insured benefits from the per-occurrence limit, or
- A combination of both of the above may occur, or the capped large loss plus the small losses still results in a loss amount over the maximum ratable loss. In this case, although the insured was able to cap the large loss, it didn't change their retrospective premium. This would be an example of the overlap between the maximum premium and accident limit.
Similar situations can arise when there is a minimum premium. The underlap between the minimum premium and accident limit occurs when there is no benefit from the accident limit even when there is a large loss because the minimum premium is sufficiently high.
Just work through the logic carefully as you solve problems - all you really need is the retrospective rating formula.
Limited Table M & Lee Diagrams
The relationships found in Fisher.Visualization and Fisher.TableM apply when calculating with a Limited Table M. Figure 1 below shows the unlimited aggregate loss curve F(y) and the aggregate loss curve limited by the per-occurrence deductible (D), FD(y). The Limited Table M (Table MD) charge at entry ratio s is the area denoted by G. The Limited Table M savings at entry ratio r is the area denoted by T + U + W. The per-occurrence excess charge is the area between the two curves, that is A + E + D + P + N + L + J + W + U.
Closing Remarks
The size of the per-occurrence limit (deductible) heavily influences the distribution of primary losses. This means a Limited Table M must be calculated for each deductible offered. Usually the unlimited losses (i.e. losses before applying a per-occurrence or aggregate limit) are known which makes it straight forward to adjust the losses to the required deductible.
Loss distributions are usually positively skewed so have many small losses and few large losses. This means the variance of the loss distribution is mostly determined by the larger losses. As we lower the per-occurrence limit the severity distribution variance decreases as frequency is unchanged. This reduces the likelihood of larger limited aggregate losses so lower deductibles normally result in lower insurance charges for entry ratios greater than 1.
| Full BattleQuiz | Excel Files | Forum |
You must be logged in or this will not work.