GLM.ModelSelection

Reading: Goldburd, M.; Khare, A.; Tevet, D.; and Guller, D., "Generalized Linear Models for Insurance Rating,", CAS Monograph #5, 2nd ed., Chapter 5, Sections 1 - 5.

Synopsis: In this article you'll learn about transforming the target variable to account for large losses, catastrophes, and other features such as loss development and trend. You'll also learn what a partial residual plot is and ways to improve your model fit through analyzing these plots.

Study Tips

Despite looking relatively straightforward there is a lot of technical information here so take your time to learn it well. You should be very familiar with both the concept of a partial residual plot and how to interpret the statistical output from them. Make sure you go through the Battlecards frequently to improve your retention of the strengths and weaknesses of the methods.

Estimated study time: 8 Hours (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• How to graphically assess the fit of a variable.
• Ways to improve a variable within a GLM.

Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.)

reference	part (a)	part (b)	part (c)	part (d)
E (2018.Fall #5)	Variable fit - describe techniques	Variable fit - disadvantages of methods
E (2012.Fall #4)	GLM probability - GLM.Basics	Model improvement - argue strategy

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.

In Plain English!

Important decisions include:

1. Choice of target and predictor variables.
2. Choice of target variable distribution.
3. Choice of representation of predictor variables.

The choice of target variable depends on what you're trying to model. For a rating plan it may be pure premium, claim frequency, or claim severity, or each of the latter in separate models. Other target variables can include loss ratio or probability of a large loss. The choice is driven by data availability and modeler preferences.

Predicting Pure Premiums: You can either:

1. Build separate models for frequency and severity and then combine them.
   • The combination method depends on the choice of link function.
     • If log links are used then the relativity factors may be multiplied together.
       • If a variable is in one model but not the other (because it wasn't significant) then multiply the relativity by 1.000.
2. Model pure premium directly using the Tweedie distribution.

Question: What are some of the disadvantages of modelling frequency and severity separately?

Solution:

1. Requires more time to build two separate models and then combine them.
2. Requires additional or more granular data.
   • For instance, it's not enough to know the claim cost and exposures, you now need claim count data also. This can come with limitation such as were claims/claimants consistently counted/recognized?

Question: What are some advantages of modelling frequency and severity separately?

Solution:

1. Can see which effects drive frequency and severity separately
2. Can see which effects have strong individual components that cancel out. Although the rating variable may not be included in the final pure premium model, this knowledge may help drive business decisions.
3. Separate frequency and severity models have less variance than a single pure premium model.
   • A strong frequency response may be less significant in the pure premium model due to high severity variance. Can lead to omitting variables and under fitting when modelling pure premiums.
4. If a variable is only significant for one of frequency and severity (say frequency) yet we include it when modelling pure premiums, then the pure premium model coefficient is reacting to the spurious/random severity signal and may result in over fitting.
5. The Tweedie distribution assumes frequency and severity move in the same direction. This isn't always true and modelling separately avoids this assumption.

In general we model individual coverages separately, a model for both Bodily Injury and Comprehensive combined probably doesn't make a lot of sense. If there is sufficient data then you can model in more depth such as modelling by peril. Make sure you remember a GLM assumes the data is fully credible though...

Sometimes it's worth modelling the perils separately and then combining into an all-peril model because it can pick up on characteristics unique to each peril.

Question: How can you combine peril models to make an all-peril model?

Solution:

To make an all-peril model from individual peril models use the following steps:

1. Make predictions of expected loss for each peril on the same set of exposure data.
2. Add the peril predictions together to get an all-peril pure premium for each record.
3. Use all of the individual model predictors as inputs to a new model, whose target is the output from step 2.

This approach gives all-peril relativities implied by the underlying by-peril models. The target data in the new model is stable because it is the sum of the by-peril model outputs. So it doesn't need a lot of data. It is more important for the input data to reflect the mix of business going forward. Only using the most recent year of data is one way to do this.

Transforming the Target Variable

Large losses can significantly influence a model so it is appropriate to cap losses at a selected threshold to make the model more stable. Set the cap high enough to capture systematic variation but not too high that it captures excessive noise. Cook's distance is a useful measure for determining if capping is needed.

Catastrophic events can skew both frequency and severity, as well as undermine the assumption of independence between records in the data set. Either remove catastrophic events so you model non-catastrophic loss only, or temper the effects by reducing the weight on those variables, or reduce the magnitude of the target variable.

Losses which are expected to develop significantly should be developed to ultimate prior to modelling. If modelling pure premiums, make sure to account for IBNR (Incurred But Not Reported). When modelling severity make sure it only reflects development on known claims.

If the target variable involves premium, then on-levelling of premiums is likely necessary.

Multi-year data should have losses and exposures trended before modelling. An alternative to trending and developing the data prior to modelling is to include a temporal variable such as year in the model. This picks up effects on the target variable that are related to time and for which the underlying data has not been adjusted for. A similar approach can be taken with a catastrophe indicator.

Variables such as the above are known as control variables. They're not used in the rating algorithm but they explain variations due to effects in the data set which may not be present in the real-world application. For instance, a multi-year data set isn't really reflective of the experience for a one-year policy which the model is building.

The inclusion of control variables allows the modeler to manage these effects so they don't unduly influence parameter estimates for the predictor variables. However, using control variables doesn't guarantee success. It may still be better to use data from a large, credible source, such as industry data when developing losses to ultimate rather than relying on a control variable.

Key Point: Ultimately, the best approach is to trend, develop, and on-level the data before modelling and then include relevant control variables such as year or catastrophe indicator. Significant differences in the behaviour between years in the resulting model output can then indicate underlying issues with either trending, development, or on-levelling which can be investigated.

mini BattleQuiz 1 You must be logged in or this will not work.

Choosing a Distribution

Selection of the target variable distribution should be based on an analysis of the deviance residuals. Typical choices for claim frequency include the Poisson, negative binomial, or binomial distributions. Claim severity is often modeled with a Gamma or inverse Gaussian distribution. A binomial distribution is appropriate if you're building a logistic model.

Variable Selection

If you are updating an existing rating plan with new relativities from new data, then the set of predictor variables is already defined for you. However, when updating a rating plan, it's often a good time to look for additional variables which could add extra segmentation.

Variable significance is a key criteria for variable selection. It's measured by the p-value. The p-value tells us the probability of estimating a coefficient of that size if the true value of the coefficient is zero.

Alice: "Remember: It does not tell you the probability that the coefficient is non-zero"

There is no threshold for the p-value which says a variable should automatically be included.

Question: What are some other considerations when deciding whether to include a variable?

Solution:

• Is it cost-effective to collect the value of the rating variable for new and renewal business?
• Does the use of the variable conform to the actuarial standards of practice and regulatory environment?

Automated variable selection processes do exist to help thin out a large list of variables. This is particularly helpful when external data sources are attached to internal data.

When including a continuous variable in the model, if the model uses a log-link then it should at least be logged. This implies a linear relationship between the log of the predictor variable and the log of the mean of the target variable. Further transformation may be needed to create a better fit though.

Partial Residual Plots

Let x_j be a predictor variable and define the i ^th partial residual as [math]r_i=\left(y_i-\mu_i\right)\cdot g^\prime\left(\mu_i\right)+\beta_j\cdot x_{ij}[/math]. Here, x_ij is the value of the j ^th predictor for the i ^th record in the data set and [math]g^\prime\left(\mu_i\right)[/math] is the first derivative of the link function, so in the case of the log-link this is [math]\frac{1}{\mu_i}[/math]. We get a partial residual for each record, i, in the data set. We can repeat this for any predictor variable, x_j.

The i ^th residual is constructed as a linear equation. The term [math](y_i - \mu_i)g^\prime(\mu_i)[/math] is the constant term which describes the scaled difference between the actual i ^th target variable and the i ^th model prediction. Adding the [math]\beta_j\cdot x_{ij}[/math] term is then adding on the piece of the linear predictor which is described by the i ^th observation of the j ^th variable. So the variance of the partial residuals contains the variance unexplained by the model and the variance explained by the inclusion of the [math]\beta_j\cdot x_{ij}[/math] term in the model.

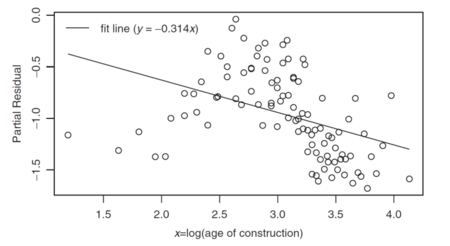
Figure 1 below is the partial residual plot for the predictor variable Age of Construction. Since Age of Construction is a continuous variable used in a log-link model it was log-transformed prior to use.

Figure 1: Source: GLM text p. 49

Observe the best fit line has slope -0.314 which is the β_j coefficient. For log of Age of Construction less than 2.5 or greater than 3.25, the best fit line is above the residuals which means the model over predicts there. The variable should be transformed further to better explain the relationship.

mini BattleQuiz 2 You must be logged in or this will not work.

(Further) Transforming Predictor Variables

There are several options for further transforming the variable:

1. Binning/banding the variable
2. Adding polynomial terms
3. Using piecewise linear functions
4. Natural cubic splines

Binning/Banding

This transforms a continuous variable into a categorical variable by dividing the range of the variable into intervals. The model then estimates a coefficient for each interval. Start by choosing the number of bins, 10 is typical. Then initialize the intervals by defining them to have approximately equal exposures or number of records per interval. Since we're moving from a continuous to a categorical variable, there is no need to log the variable before binning.

An advantage of binning is each interval has its coefficient independently estimated, there is maximal freedom.

Question: What are four disadvantages of binning a variable?

Solution:

Disadvantages of binning include:

1. It introduces a lot of coefficients (one for each interval). This can violate parsimony which is the idea that the model should be kept as simple as possible.
   • That is, it increases the risk of over fitting.
2. Estimates are not guaranteed to be continuous. The coefficients are derived independently so random noise can distort the pattern of coefficients across several intervals.
3. Estimates can produce counter-intuitive results which don't make business sense. For instance, if amount of insurance is binned, it may indicate $400,000 as having a lower pure premium than $300,000 even though we know a loss costs more on average when the amount insured is higher.
   • When you bin the data, you get independent estimates for each of the coefficients regardless of if you believe they should have a natural order.
4. Variation within intervals is ignored because each bin gets a single estimate regardless of the range of the interval.
   • Bins could be subdivided further but than the data in each bin becomes less credible, causing the coefficients to have larger error bars.

Some of these issues can be overcome by manual smoothing during the final factor selection process.

Adding Polynomial Terms

We can add terms such as square, cubic, or higher order terms to form a higher degree polynomial equation for the variable in question. This generally gives a much better fit but risks over fitting the data to the training data set because each term added has its own independently estimated coefficient. Another limitation is it's hard to interpret the relationship between the target and predictor variables from the coefficients alone.

Question: What are two drawbacks of using additional polynomial terms?

Solution:

• Loss of Interpretability: It may be difficult to understand the relationship between the target variable and the predictor by looking at the coefficients alone. You may need to graph the function.
• Erratic end scale behavior: As more terms are included in the polynomial, the graph of the function may turn sharply up or down at the extremes of the data. This behavior is unlikely to be reflective of reality.

Using Piecewise Linear Functions

To improve the fit, we can break a linear function into several pieces by defining new variables. The new variables allow the slope of the line to change as we progress through the original continuous variable. The new variable is known as a hinge function. It is defined as [math]\max(0,x-a)[/math] where x is the original variable and a is the break point which is the place where you want to change the function used. Unlike binning, the predictor variable is first logged if a log link function is used. That is, transform your variable before breaking into pieces.

To break the line into n pieces we need [math]n-1[/math] hinge functions. All are defined in the same manner, just with different a values. Let's continue looking at the Age of Construction example from the text (refer to Figure 1).

Our continuous predictor variable is the Age of Construction (AoC) and we're using a log-link function. So our first step is to take [math]\ln(AoC)[/math]. We now choose hinge points by looking at the partial residual plot. In [math]\ln(AoC)[/math] terms, there appear to be changes in the pattern at 2.75 and 3.5. These will be our two hinge points. We get three functions: [math]\ln(AoC), \max(0,\ln(AoC)-2.75), \max(0, \ln(AoC)-3.5)[/math]. Suppose we get the following statistical output:

Variable	Estimate	Std. Error	p-value
[math]\ln(AoC)[/math]	1.289	0.159	<0.0001
[math]\max(0,\ln(AoC)-2.75)[/math]	-2.472	0.315	<0.0001
[math]\max(0,\ln(AoC)-3.5)[/math]	1.170	0.0079	0.0042

The small p-values indicate a good reason for the change. The second split at 3.5 has a bigger p-value than the split at 2.75 which suggests it is slightly less relevant but is still significant. We now need to determine the slope of each linear function.

For ln(AoC) less than 2.75, only [math]\ln(AoC)[/math] is non-zero. In this case the slope is 1.289.

For ln(AoC) values between 2.75 and 3.5, both [math]\ln(AoC)[/math] and [math]\max(0,\ln(AoC))[/math] are non-zero. Since we're using logged values, the slope is obtained by adding the two estimates together, so [math]1.289+ -2.472 = -1.183[/math]. For the values of ln(AoC) after 3.5, all three functions are non-zero so we add the three estimates together to get [math]1.289+-2.472+1.170 = -0.013[/math]. So we've fitted a piecewise linear curve which increases steeply from 0 to [math]e^{2.75}[/math], then declines rapidly from there to [math]e^{3.5}[/math] and then weakly declines for the rest.

A significant drawback of using hinge functions is the break points are not automatically determined by the GLM. It is customary to estimate the break points from the partial residual plot and then refine them by perturbing them in a way which improves the model fit. There are variations of GLMs which automate hinge point selection but these are beyond the scope of Exam 8.

Natural Cubic Splines

Natural cubic splines are a combination of polynomial functions and piecewise functions which can improve the fit of non-linear effects. Some key characteristics are:

• The first and second derivatives of a natural cubic spline are continuous. This means the curve appears smooth (great for reducing the risk of illogical rating).
• A linear fit is used before the first break point and after the last break point. This reduces the erratic behavior seen at the extremes when higher order polynomials are used.
• Using break points allows different polynomials to pick up different responses in different parts of the predictor variable rather than trying to find one polynomial which fits well across the entire domain of the predictor variable. This is particularly useful for fitting to data with cyclical effects.

However, it's important to remember that natural cubic splines are hard to interpret from their coefficients alone; plotting the curve is often required to understand the modeled relationship between the predictor and target variables.

mini BattleQuiz 3 You must be logged in or this will not work.

Grouping Categorical Variables

Some categorical variables have a few levels (binary indicators for instance) while others have many levels (e.g. whole years of driving experience). When using categorical variables with lots of levels, it is important to group levels to avoid having too many degrees of freedom. Too many degrees of freedom can lead to over fitting, model instability and results that don't make sense.

One way to handle grouping is to start with many levels and compare the estimated coefficients for neighboring buckets. If bucket A–B and bucket C–D have similar coefficients then create a new bucket, A–D so that the number of levels in the variable decreases by one. Note this approach works with grouping buckets from continuous variables, you can group say age of home "30-39" with "40-49" to produce a single "30-49" category.

This is typically an iterative process which depends on balancing the risk of overfitting against keeping the model simple (parsimony) while maximizing the predictive power of the model.

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.