Holmes.Diagnostics
Reading: Holmes, T. & Casotto, M, “Penalized Regression and Lasso Credibility,” CAS Monograph #13, November 2024. Chapter 6.
Synopsis: In this article we explore how to review lasso credibility models and briefly contrast this with reviewing a GLM. The focus shifts from variable significance (GLMs) to reviewing the actuarial appropriateness of the chosen complement of credibility and assessing the validity of the selected lambda penalty parameter. We introduce the concept of relativity plots which are used to examine the movement of the model output between the offset, observed relativity, and GLM output.
Study Tips
- This is core material for the monograph. Expect to be given some form of relativity plot to review and probably some short answer or multiple choice questions. It's hard to see how they can ask calculation questions on this section though.
Estimated study time: 1 Hour (not including subsequent review time)
BattleTable
Based on past exams, the main things you need to know (in rough order of importance) are:
- Know how to interpret a relativity plot .
- Explain how to review a lasso credibility model by variable type and level of assigned credibility.
- Explain why the review process focuses on the lambda parameter and actuarial appropriateness of the complement of credibility.
Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.)
reference part (a) part (b) part (c) part (d) Currently no prior exam questions
| Full BattleQuiz | Excel Files | Forum |
You must be logged in or this will not work.
In Plain English!
Reviewing either a (lasso) penalized regression model or a lasso credibility model is distinctly different to reviewing a traditional GLM. For one - there are no p-values! We must focus on thinking about credibility rather than variable significance. This means focusing on evaluating the lambda penalty parameter used to assign credibility.
Question: Briefly explain the difference in review style between reviewing a GLM and reviewing (lasso) penalized regression.
- Solution: Reviewing a GLM focuses on whether variables and coefficients are significant. Whereas reviewing a (lasso) penalized regression model focuses on understanding how much we can trust the subject experience (modeling data set).
Question: Briefly describe three questions to ask when reviewing the penalty term in a penalized regression model.
- Solution:
- Was the lambda parameter selected via cross-validation or another robust methodology?
- If there was an adjustment to the lambda penalty parameter, was the adjustment favoring a more robust model (increasing the penalty parameter) and why was the adjustment made?
- Do the variables behave in an intuitive way which is consistent with the selected lambda parameter?
Holmes and Casotto offer a version of the following table which compares what happens in a GLM vs lasso credibility by variable importance.
Variable Importance GLM Lasso Credibility High Full credibility is assigned to the observed relativity Credibility is assigned more to the observed experience than the complement of credibility. Medium Full credibility is assigned to the observed relativity during model fitting. Manual adjustments may be appropriate for p-values near 0.05 (or other chosen significance threshold). Credibility is assigned more to the complement of credibility than the observed experience. Low Subjective decision rule, i.e., remove when p-value > 0.05. Automatically set coefficient to 0.0.
Lasso credibility removes the need to perform post-hoc significance testing which saves significant effort. However, it's important that you review the appropriateness of the complement of credibility.
Reviewing the Complement of Credibility
You should follow the guidance provided in ASOP25.Credibility when reviewing credibility in any context. Since that guidance is covered elsewhere, we focus on the aspects which are unique to the lasso credibility procedure.
A strength of the lasso credibility procedure is its multivariate nature. This means we need to consider the correlations between the risk characteristics. In particular, introducing offsets can limit the model's ability to correctly assign signal between correlated predictors.
Correlated risk characteristics can pose additional problems if their offsets (complements of credibility) come from different sources — for example, you may use your prior rating plan relativities for an existing variable and a competitor's relativities for a new variable which is correlated to an extent with your existing rating plan.
Holmes and Casotto recommend using relativity plots to identify segments where you need to spend time looking at both the complement of credibility and the model output.
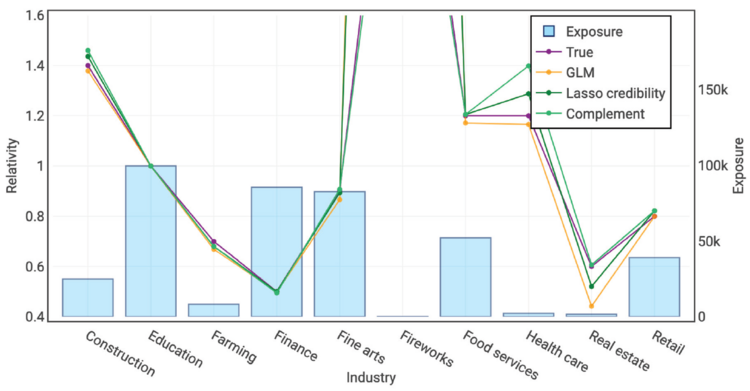
Relativity Plots
Below is an example of a relativity plot taken directly from the source.
This is very similar to the plots we've already seen when we were looking at the effect of various penalty parameter sizes. In a relativity plot we show the following for each category within a rating variable:
- The complement of credibility (the offset).
- The indicated relativity (model relativity which is the combination of the fixed and variable components, labelled above as Lasso Credibility).
- The observed relativity (labelled above as TRUE). This is optional to show.
- The GLM relativity - this is optional to show but helps you assess the movement due to the assigned credibility.
- Exposures on the secondary axis.
Alice: "Pay attention! We're working with relativities here so you must transform all of the offsets and coefficients by inverting the link function."
When producing relativity plots it's important to include all transformations of a rating variable when creating the final relativity. For example, when modeling Age using a third-degree polynomial, we would want to combine the relativities for the Age, Age2, and Age3 variables to see the full picture. This means we need to carefully consider any interactions used in the model.
Lasso credibility is a function of both the negative log-likelihood and the penalty term. The former varies with the number of exposures as when there are fewer exposures it may be easier for the penalty term to dominate. Including the exposures in the relativity plot helps the reviewer assess whether the underlying experience supports the deviation from the complement of credibility.
When reviewing relativity plots we are aiming to address the following question: Are the deviations from the complement of credibility stable and intuitive across all variables?
Stable and intuitive are relative terms which may vary between models and even within models by rating variable.
mini BattleQuiz 1 You must be logged in or this will not work.
Full Credibility in the Complement
Question: Identify two scenarios where lasso credibility will assign full credibility to the complement.
- Solution:
- When there is sufficient exposure to model but the experience is too similar to the complement of credibility to deviate.
- When there is insufficient data in a segment to pass the lasso credibility threshold.
The first scenario doesn't require much review. It just happens the experience in the modeling data set is very similar to the complement so produced the same output as the complement. Since we know there is a credible volume of data underpinning the result no further review is needed.
The second scenario results in the complement receiving full credibility even if the complement is inappropriate. Segments with limited exposure should expect to see large differences between the observed relativity and the offset (complement) — this doesn't mean the complement is inappropriate, nor does a small difference mean a complement is appropriate. When exposure volumes are low it's best to rely on traditional actuarial considerations to assess if the complement is appropriate. This is review is important because an inappropriate complement may expose you to adverse selection, restrict growth, or unreasonably burden policyholders.
Partial Credibility in the Complement
It's more common for the complement to receive partial credibility with the predicted relativity lying somewhere between the observed and complement.
Question: Identify two scenarios where the complement receives partial credibility.
- Solution:
- A specific segment has a medium amount of data, passing the lasso credibility significance threshold but not enough to materially deviate from the complement.
- When the entire data set is smaller than necessary to achieve full credibility.
Holmes and Casotto claim small differences between the complement and indicated relativities are most often an ideal result in a lasso credibility model. This is because they have overcome the penalty term (lasso credibility standard) to reflect partial credibility. If the deviations are proportional to the exposure volume and reasonable given the complement relativities then the assigned credibility is likely appropriate.
Contrast this with a GLM where small coefficients are often carefully looked at because it can be hard to reject the null hypothesis that the true coefficient is zero.
Holmes and Casotto recommend focusing your time on segments (categories) with medium or small amounts of data which have large differences between the complement and indicated relativities. Large differences may imply the penalty parameter needs to be increased. They may also indicate outliers in the modeling data set, particularly if the large differences occur in single categories or unexpected places.
Large differences between the complement and indicated relativities are supportable, especially if the deviation is actuarially intuitive and the rest of the coefficients have reasonable behavior.
If the entire modeling data set is smaller than necessary to achieve full credibility then it's very important to review both coefficient stability and the intuitiveness of the results. When many coefficients produce unintuitive results its a good sign the penalty parameter is too small.
Small data sets present the greatest problems to a modeler because the choice of complement and penalty term have an outsized impact on the model output.
Limited or No Credibility in the Complement
When a category has a substantial exposure the complement may receive little to no credibility. Large deviations from the complement should still be investigated but it's unlikely that changing the complement would materially alter the model output.
Therefore, you should focus on variables and/or categories which have limited exposures and have large deviations from their complement. This is often an indicator that the penalty parameter is too small.
mini BattleQuiz 2 You must be logged in or this will not work.
Review by Variable Type
Categorical Variables
With lasso credibility, categories should be at least as granular as the chosen complement of credibility because when a category is insignificant it will have its coefficient reduced to zero so we pick up the complement relativity. This removes the need to group non-credible categories. In contrast, in a GLM we must manually group insignificant levels with the base level and refit the model to obtain stable coefficients.
When reviewing categorical variables in a lasso credibility procedure you must assess whether the deviation from the complement is directionally appropriate and if the magnitude of the deviation is sufficiently responsive.
Continuous Variables
Continuous variables are highly discouraged from use in a lasso credibility model. They are difficult to conceptualize because the slope is penalized rather than the magnitude of differences between categories.
That said, if you have a continuous variable in your lasso credibility model then you'll want to focus your review on the following:
- The ability of continuous transformation to accurately capture potential differences from the complement. For example, including a linear variable allows the model to identify a change in the overall slope but not a hinge or change in the slope after a certain point.
- Whether it is appropriate to extrapolate continuous variables to levels where there is minimal credibility.
Ordinal Variables
These are straightforward to review and are helpful to look at when determining an appropriate penalty parameter. It's common to start with the indicated optimal penalty parameter and then look at ordinal variables for reversals. If there are reversals present then the penalty parameter is probably too small and should be increased until the reversals are no longer present in the model. This usually produces a model which is actuarially and statistically sound.
An uncapped continuous variable often extrapolates wildly in the tails, beyond what is implied by the data. In contrast, an ordinal variable does not go beyond what is indicated by the data as it is pulled towards the complement when the data is thin. This means the modeler may need to select an appropriate extrapolation for ordinal variables in the tail.
Control Variables
Alice: "In my opinion this section of the text isn't well written. What follows is my understanding of what the authors are trying to convey. I recommend you read the source (less than half a page) and see if you agree with me."
As we discussed earlier, control variables are used to prevent signals from flowing into other characteristics. The question we attempt to address here is whether control variables should be included in lasso credibility via a fixed component or whether there should also be a variable component (Click here for a refresher on fixed and variable components).
According to Holmes and Casotto this is a judgment call for the modeler to make. If we include a variable component then the lasso credibility model will pick up any significant deviations from the control level. It's straightforward to include some control variables as the complement (fixed component) is often known; for example, in a countrywide model we may control for State variations through including the current State relativity as a fixed component. If we add in a variable component for State then we allow the lasso credibility model to alter the State relativity to reflect significant state-level differences found in our data set.
Other control variables are more challenging to include in a lasso credibility model. For example, if you have a multi-year dataset then loss trend and development issues are likely present as well as things like potential changes to the legal environment. The question is what is the appropriate complement of coefficient to include when attempting to control for Year? In this situation we cannot draw upon a prior rate manual relativity as one doesn't exist!
One option is to include control variables in the lasso credibility model with no fixed component (offset coefficient of zero). Then the model will automatically remove insignificant control variables and its unlikely they would have had a material impact on other variables.
On the flip side, if we include control variables with an appropriate complement (fixed component) and no variable component then the lasso credibility model will alter the rest of the model's variable components to best reflect the available signal, even if this means picking up some of the control variable signal in another variable.
Overall, it's definitely a matter of judgment and possibly time/available computing power if you want to try out several of the approaches.
Conclusions
Lasso credibility models change the focus of model review from significance of variables to the credibility associated with the data. This simplifies the review process.
The inclusion of a complement of credibility for each rating variable introduces a bias towards the complement which is why we must devote more review time to assessing the actuarial appropriateness of the complement.
A lasso credibility model with only categorical or ordinal variables is straightforward to review as you only need focus on determining a reasonable penalty parameter, [math]\lambda[/math], provided the variables are sufficiently granular. Such review is limited if cross-validation is used to produce the optimal lambda parameter which is then tuned (adjusted higher) to produce actuarially sound relativities.
| Full BattleQuiz | Excel Files | Forum |
You must be logged in or this will not work.