Fisher.TableL: Difference between revisions
m (→BattleTable) |
No edit summary |
||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
'''Reading''': Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 5 | '''Reading''': Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 5 | ||
'''Synopsis''': This article goes over the second approach for handling policies which have both a per-occurrence limit/deductible and an aggregate limit/deductible. Although we treat both limits/deductibles at once, the process follows a similar pattern to what we learned in [[Fisher.TableM]] and [[Fisher.LimitedTableM]] | '''Synopsis''': This article goes over the second approach for handling policies which have both a per-occurrence limit/deductible and an aggregate limit/deductible. Although we treat both limits/deductibles at once, the process follows a similar pattern to what we learned in ''[[Fisher.TableM]]'' and ''[[Fisher.LimitedTableM]]''. | ||
==Study Tips== | ==Study Tips== | ||
| Line 9: | Line 7: | ||
This material is less tested so focus on being able to explain the differences between the methods and knowing how to set up the calculations. You should also make sure you know the ICRLL procedure and why is was needed, even though it's pretty much become outdated as there's sufficient computing power to build as many limited or unlimited Table M's as needed. | This material is less tested so focus on being able to explain the differences between the methods and knowing how to set up the calculations. You should also make sure you know the ICRLL procedure and why is was needed, even though it's pretty much become outdated as there's sufficient computing power to build as many limited or unlimited Table M's as needed. | ||
'''Estimated study time''': | '''Estimated study time''': 8 Hours ''(not including subsequent review time)'' | ||
==BattleTable== | ==BattleTable== | ||
| Line 17: | Line 15: | ||
* How to <span style="color:green;">'''build a Table L'''</span> and calculate its insurance charges and savings. | * How to <span style="color:green;">'''build a Table L'''</span> and calculate its insurance charges and savings. | ||
* Describe and apply the <span style="color:blue;">'''ICRLL procedure'''</span>. | * Describe and apply the <span style="color:blue;">'''ICRLL procedure'''</span>. | ||
{|class="wikitable" | |||
|- | |||
| Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.) | |||
|} | |||
: {| class='wikitable' style='width: 1000px;' | : {| class='wikitable' style='width: 1000px;' | ||
| Line 32: | Line 35: | ||
|- style="border-bottom: 2px solid;" | |- style="border-bottom: 2px solid;" | ||
|| [https://www.battleacts8.ca/8/pdf/Exam_(2016_2-Fall)/(2016_2-Fall)_(14).pdf <span style='font-size: 12px; background-color: yellow; border: solid; border-width: 1px; border-radius: 5px; padding: 2px 5px 2px 5px; margin: 5px;'>E</span>] <span style='color: red;'>'''(2016.Fall #14)'''</span> | || [https://www.battleacts8.ca/8/pdf/Exam_(2016_2-Fall)/(2016_2-Fall)_(14).pdf <span style='font-size: 12px; background-color: yellow; border: solid; border-width: 1px; border-radius: 5px; padding: 2px 5px 2px 5px; margin: 5px;'>E</span>] <span style='color: red;'>'''(2016.Fall #14)'''</span> | ||
| style="background-color: lightgrey;" | ''Lee Diagrams'' <br> [[Fisher.Visualization]] | | style="background-color: lightgrey;" | ''Lee Diagrams'' <br> ''[[Fisher.Visualization]]'' | ||
|| '''Overlap''' <br> - compare Tables M and L | || '''Overlap''' <br> - compare Tables M and L | ||
|| '''Workers' Comp''' <br> - recommend Table M or L | || '''Workers' Comp''' <br> - recommend Table M or L | ||
| Line 67: | Line 70: | ||
|} | |} | ||
[https:// | <!-- ******** BattleBar Code ******** --> | ||
{|style="border: solid; color:lightgrey; border-radius:10px; border-width:2px; align:center;" | |||
: [ | |- | ||
<!-- ******** Full BattleQuiz ******** --> | |||
: [https://battleacts8.ca/8/forum/index.php?p=/categories/ | |style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''Full BattleQuiz]'''</span> | ||
<!-- --> | |||
<!-- ******** Excel BattleQuiz ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="color: red; font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; border-color: darkblue; padding: 2px 10px 2px 10px; margin: 0px;">'''''Excel BattleQuiz]'''''</span> | |||
--> | |||
<!-- --> | |||
<!-- ******** Excel PowerPack Files ******** --> | |||
|style="padding:2px"|[[BattleActs_PowerPack#ppFisher| <span style="color: white; font-size: 12px; background-color: indigo; border: solid; border-width: 2px; border-radius: 10px; border-color: indigo; padding: 1px 3px 1px 3px; margin: 0px;">'''''Excel Files '''''</span>]] | |||
<!-- --> | |||
<!-- ******** Forum ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/index.php?p=/categories/fisher-tablel<span style="font-size: 12px; background-color: lightgrey; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Forum'''</span>] | |||
<!-- --> | |||
<!-- ******** Formula Sheet ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/categories/fisher-tablel<span style="font-size: 12px; color: darkblue; background-color: lightblue; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Formula Sheet'''</span>] | |||
--> | |||
|} | |||
<span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | |||
==In Plain English!== | ==In Plain English!== | ||
| Line 106: | Line 127: | ||
: <span class="newwin">[https://www.battleacts8.ca/8/pdf/Fisher_Ch3Q14practice.pdf <span style="color: white; font-size: 12px; background-color: green; border: solid; border-width: 2px; border-radius: 10px; border-color: green; padding: 1px 3px 1px 3px; margin: 0px;">'''''One problem like Chapter 3 Question 14'''''</span>]</span> | : <span class="newwin">[https://www.battleacts8.ca/8/pdf/Fisher_Ch3Q14practice.pdf <span style="color: white; font-size: 12px; background-color: green; border: solid; border-width: 2px; border-radius: 10px; border-color: green; padding: 1px 3px 1px 3px; margin: 0px;">'''''One problem like Chapter 3 Question 14'''''</span>]</span> | ||
[https:// | [https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=1<span style="font-size: 20px; background-color: aqua; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''mini BattleQuiz 1]'''</span> <span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | ||
===How to Build a Table L Using Empirical Data=== | ===How to Build a Table L Using Empirical Data=== | ||
| Line 113: | Line 134: | ||
# Compute the entry ratio for each risk in the group of risks. The entry ratio is the ratio of actual limited losses to expected unlimited losses. | # Compute the entry ratio for each risk in the group of risks. The entry ratio is the ratio of actual limited losses to expected unlimited losses. | ||
#* If necessary, re-order the risks in the group so the entry ratios are in <u>increasing</u> order. | #* If necessary, re-order the risks in the group so the entry ratios are in <u>increasing</u> order. | ||
# Apply the [[Fisher.TableM#Building a Table M |<u>'''horizontal slicing method'''</u>]] to calculate <math>\phi_D^\star(r)-k</math>. | # Apply the ''[[Fisher.TableM#Building a Table M |<u>'''horizontal slicing method'''</u>]]'' to calculate <math>\phi_D^\star(r)-k</math>. | ||
# Add the excess ratio on to price the total loss cost for the entry ratio. | # Add the excess ratio on to price the total loss cost for the entry ratio. | ||
# Use <math>\psi_D^\star(r)=\phi_D^\star(r)+r-1</math> to compute the insurance savings to complete the table. | # Use <math>\psi_D^\star(r)=\phi_D^\star(r)+r-1</math> to compute the insurance savings to complete the table. | ||
| Line 128: | Line 149: | ||
This allows you to correctly apply the per-occurrence limit. It is not enough to know the parameterized form of the unlimited aggregate loss distribution and the excess ratio. | This allows you to correctly apply the per-occurrence limit. It is not enough to know the parameterized form of the unlimited aggregate loss distribution and the excess ratio. | ||
[https:// | [https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=2<span style="font-size: 20px; background-color: aqua; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''mini BattleQuiz 2]'''</span> <span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | ||
===The Insurance Charge Reflecting Loss Limitation (ICRLL) Method=== | ===The Insurance Charge Reflecting Loss Limitation (ICRLL) Method=== | ||
| Line 192: | Line 213: | ||
: We assume the state/hazard group in question has a severity distribution that is closely related to the severity distribution of the Table M used, i.e. the distributions only differ in scale. | : We assume the state/hazard group in question has a severity distribution that is closely related to the severity distribution of the Table M used, i.e. the distributions only differ in scale. | ||
[https:// | [https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=3<span style="font-size: 20px; background-color: aqua; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''mini BattleQuiz 3]'''</span> <span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | ||
[https:// | <!-- ******** BattleBar Code ******** --> | ||
{|style="border: solid; color:lightgrey; border-radius:10px; border-width:2px; align:center;" | |||
: [https://battleacts8.ca/8/forum/index.php?p=/categories/ | |- | ||
<!-- ******** Full BattleQuiz ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 10px;">'''Full BattleQuiz]'''</span> | |||
<!-- --> | |||
<!-- ******** Excel BattleQuiz ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/FC.php?selectString=**&filter=both&sortOrder=natural&colorFlag=allFlag&colorStatus=allStatus&priority=importance-high&subsetFlag=miniQuiz&prefix=Fisher&suffix=TableL§ion=all&subSection=all&examRep=all&examYear=all&examTerm=all&quizNum=all<span style="color: red; font-size: 20px; background-color: lightgreen; border: solid; border-width: 1px; border-radius: 10px; border-color: darkblue; padding: 2px 10px 2px 10px; margin: 0px;">'''''Excel BattleQuiz]'''''</span> | |||
--> | |||
<!-- --> | |||
<!-- ******** Excel PowerPack Files ******** --> | |||
|style="padding:2px"|[[BattleActs_PowerPack#ppFisher| <span style="color: white; font-size: 12px; background-color: indigo; border: solid; border-width: 2px; border-radius: 10px; border-color: indigo; padding: 1px 3px 1px 3px; margin: 0px;">'''''Excel Files '''''</span>]] | |||
<!-- --> | |||
<!-- ******** Forum ******** --> | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/index.php?p=/categories/fisher-tablel<span style="font-size: 12px; background-color: lightgrey; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Forum'''</span>] | |||
<!-- --> | |||
<!-- ******** Formula Sheet ******** --> | |||
<!-- | |||
|style="padding:2px"|[https://battleacts8.ca/8/forum/categories/fisher-tablel<span style="font-size: 12px; color: darkblue; background-color: lightblue; border: solid; border-width: 1px; border-radius: 10px; padding: 2px 10px 2px 10px; margin: 0px;">'''Formula Sheet'''</span>] | |||
--> | |||
|} | |||
<span style="color: red;">'''You must be <u>logged in</u> or this will not work.'''</span> | |||
==Pop Quiz Answers== | ==Pop Quiz Answers== | ||
| Line 202: | Line 243: | ||
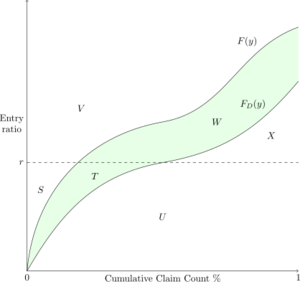
To prove the relationship it is helpful to observe the area under ''F(y)'' equals 1 so <math>T+W+U+X=1</math>. Similarly, the entry ratio ''r'' creates a rectangle of area ''r'' so <math>r=S+T+U</math>. Then <math>\begin{align}\phi_D^\star(r) +r-1 &= (X+T+W) +(S+T+U) - (T+W+X+U) \\ &= S+T \\ &= \psi_D^\star(r).\end{align}</math> | To prove the relationship it is helpful to observe the area under ''F(y)'' equals 1 so <math>T+W+U+X=1</math>. Similarly, the entry ratio ''r'' creates a rectangle of area ''r'' so <math>r=S+T+U</math>. Then <math>\begin{align}\phi_D^\star(r) +r-1 &= (X+T+W) +(S+T+U) - (T+W+X+U) \\ &= S+T \\ &= \psi_D^\star(r).\end{align}</math> | ||
[[#PopQuiz1 |Go Back]] | ''[[#PopQuiz1 |Go Back]]'' | ||
Latest revision as of 10:45, 20 May 2024
Reading: Fisher, G. et al, "Individual Risk Study Note," CAS Study Note, Version 3, October 2019. Chapter 3. Section 5
Synopsis: This article goes over the second approach for handling policies which have both a per-occurrence limit/deductible and an aggregate limit/deductible. Although we treat both limits/deductibles at once, the process follows a similar pattern to what we learned in Fisher.TableM and Fisher.LimitedTableM.
Study Tips
This material is less tested so focus on being able to explain the differences between the methods and knowing how to set up the calculations. You should also make sure you know the ICRLL procedure and why is was needed, even though it's pretty much become outdated as there's sufficient computing power to build as many limited or unlimited Table M's as needed.
Estimated study time: 8 Hours (not including subsequent review time)
BattleTable
Based on past exams, the main things you need to know (in rough order of importance) are:
- How to build a Table L and calculate its insurance charges and savings.
- Describe and apply the ICRLL procedure.
| Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.) |
reference part (a) part (b) part (c) part (d) E (2017.Fall #17) ICRLL procedure
- calculateICRLL procedure
- describeE (2016.Fall #14) Lee Diagrams
Fisher.VisualizationOverlap
- compare Tables M and LWorkers' Comp
- recommend Table M or LE (2014.Fall #12) Table L charges
- calculateTable L savings
- describeE (2013.Fall #13) Table L charges
- draw relationshipTable L charges
- describe relationshipE (2013.Fall #19) ICRLL procedure
- calculateICRLL procedure
- explainE (2012.Fall #18) Table L
- construct
| Full BattleQuiz | Excel Files | Forum |
You must be logged in or this will not work.
In Plain English!
A (California) Table L is used to estimate the per-occurrence charge and aggregate excess charge together in a single table. The entries in a Table L are organized by policy size, entry ratio and per-occurrence limit (deductible). The Table L entry ratio is defined as [math]r=\frac{\mbox{actual }{\color{red}\textbf{limited}}\mbox{ aggregate losses}}{\mbox{expected }{\color{red}\textbf{unlimited}} \mbox{ aggregate losses}}[/math]. Note that in the entry ratio for a Limited Table M both the numerator and denominator were limited.
The Table L insurance charge at entry ratio r is denoted by [math]\phi_D^\star (r)[/math] and is the average difference between a risk's actual unlimited loss and its actual loss limited to D plus the limited loss greater than [math]r\cdot E[/math]. Here E is the unlimited expected loss. The superscript * and subscript D tells us the entry ratio is for a Table L with per-occurrence limit D.
The Table L insurance savings, [math]\psi^\star_D(r)[/math], is the average amount by which the risk's actual limited loss is less than [math]r\cdot E[/math]. The Table L insurance charge and insurance savings are a ratio to expected unlimited loss. This means the loss cost is given by [math]\phi^\star_D(r)\cdot E[/math].
Recall Y is the distribution of unlimited losses and its cumulative distribution is F(y). Then FD(y) is the cumulative distribution of Y restricted by the per-occurrence limit, i.e. the cumulative distribution of the primary layer of losses. Then [math]\phi_D^\star (r) =\displaystyle\int_r^\infty (y-r)\mathrm{d}F_D(y)+k[/math], where [math]k=\frac{E-E[A_D]}{E}[/math] is the excess ratio for the per-occurrence limit. The Table L insurance savings is [math]\psi_D^\star(r)= \int_0^r(r-y)\mathrm{d}F_D(y)[/math]. These formulas avoid double counting losses because they use the limited cumulative distribution FD(y) and the excess ratio, k.
It can be helpful to view a Lee diagram of the situation when there is both a per-occurrence limit and an aggregate limit (see Figure 1 below).
The region T + W represents the per-occurrence excess losses, so [math]T+W=k[/math]. The area U + X is the primary loss distribution, i.e. losses used to price the aggregate excess limit. Region X is the aggregate loss distribution in excess of the aggregate limit. Summing gives the insurance charge for the policy as [math]\phi_D^\star(r)=X+T+W[/math]. The Table L insurance savings, [math]\psi_D^\star(r)[/math], is the region S + T. These regions should be compared to the case when there is only an aggregate limit, in which case [math]\phi(r)=W+X[/math] and [math]\psi(r)=S[/math]. Lastly, the relationship between the insurance savings and insurance charge still holds true for a Table L, namely [math]\psi_D^\star(r)=\phi_D^\star(r)+r-1[/math].
|
Can you prove [math]\psi_D^\star(r)=\phi_D^\star(r)+r-1[/math] using the Lee diagram? Click for Answer |
Here's a great question from the end of section problems in the text. Alice has got you covered with a custom solution.
To make sure you've got this, here's a practice version.
mini BattleQuiz 1 You must be logged in or this will not work.
How to Build a Table L Using Empirical Data
To build a Table L using empirical data you need both the unlimited losses and losses limited by the per-occurrence limit for a group of risks which have similar size and the same per-occurrence limit. Here's the procedure:
- Compute the excess ratio [math]k=\frac{E-E[A_D]}{E}[/math]. This is fixed for all risks in the group.
- Compute the entry ratio for each risk in the group of risks. The entry ratio is the ratio of actual limited losses to expected unlimited losses.
- If necessary, re-order the risks in the group so the entry ratios are in increasing order.
- Apply the horizontal slicing method to calculate [math]\phi_D^\star(r)-k[/math].
- Add the excess ratio on to price the total loss cost for the entry ratio.
- Use [math]\psi_D^\star(r)=\phi_D^\star(r)+r-1[/math] to compute the insurance savings to complete the table.
To see this in action, here's the example used in the text.
If we have claim level unlimited losses (as opposed to risk/policy level losses) then we can calculate a Table L for any desired per-occurrence limit (deductible).
Using Simulated Data to Build a Table L
To simulate data for a Table L you need to separately do two things:
- Simulate the number of claims,
- Simulate the severity of each claim.
This allows you to correctly apply the per-occurrence limit. It is not enough to know the parameterized form of the unlimited aggregate loss distribution and the excess ratio.
mini BattleQuiz 2 You must be logged in or this will not work.
The Insurance Charge Reflecting Loss Limitation (ICRLL) Method
Although computing power and data storage is readily available today, historically Table M and Limited Table M were printed. Rather than producing multiple Limited Table M's for various per-occurrence limits (deductibles) it is (was) often easier to use a process to modify Table M to approximate the Limited Table M for a given per-occurrence limit (deductible).
The Fisher text demonstrates an example of this using the 1998 NCCI Table M which is arranged by Expected Loss Group (ELG) instead of expected number of claims. Adjustments are made by state and hazard group to account for differences in severity between risks within an expected loss group.
Recall a Limited Table M is defined by three characteristics: expected limited loss, entry ratio, and deductible; whereas Table M is defined by two characteristics: expected unlimited loss and entry ratio. The ICRLL method may be viewed as mapping the Limited Table M onto Table M. To do so, modifications are required to the Limited Table M entry ratio and expected loss group. Here's how to apply the ICRLL method:
- Compute the entry ratio which is the actual limited aggregate loss divided by the expected limited aggregate loss. (Remember: we're working with a Limited Table M.)
- Compute the excess ratio [math]k=\frac{E-E[A_D]}{E}[/math].
- Compute the ICRLL adjustment, [math]\mathrm{ICRLL}=\frac{1+0.8\cdot k}{1-k}[/math].
- Compute the Adjusted Expected Loss = (Expected unlimited aggregate loss) * (state/hazard group adjustment) * (ICRLL).
- Find the expected loss group that contains the adjusted expected loss.
- Find the insurance charge in Table M by looking up the value determined by the entry ratio and expected loss group.
- Calculate the aggregate limit charge using [math]\phi(r)\cdot E[A_D][/math].
- Calculate the per-occurrence limit charge using [math]E-E[A_D][/math].
- Calculate the total loss cost of the policy by summing the per-occurrence and aggregate charges.
| Key Point: Since we're pricing a policy we don't know the actual limited loss (yet); replace it with the aggregate policy limit in the entry ratio calculation. |
To see this in action, here's the example used in the text.
Alice: "One of the ways the CAS can make this type of question harder is by not explicitly giving you all of the information you require. For instance, they may not give you both the expected limited and unlimited loss and instead give you the excess loss factor and the expected unlimited loss.
It's helpful to recall the excess loss factor is [math]\frac{E-E[A_D]}{\mbox{Standard Premium}}[/math] so by dividing the top and bottom of the excess ratio formula, k, by the standard premium we can write [math]k=\frac{\mbox{Excess Loss Factor}}{\mbox{(Ultimate) Loss Ratio}}[/math]."
Question: What are two advantages of using the ICRLL procedure?
- Solution:
- Allows a single unlimited Table M to produce any number of Limited Table M's which are reasonably accurate. This reduced the need for producing and storing lots of large Limited Table M's.
- Provides a good approximation so if a book of business A lacks data, you can adjust the Table M for a similar book of business (B) to produce Table M's for book of business A.
Question: What is a disadvantage of using the ICRLL procedure?
- Solution:
- Since the ICRLL procedure is an approximation, it can introduce errors in the estimated insurance charge and savings.
Question: Why does the ICRLL procedure include an adjustment for the state/hazard group?
- Solution:
- The state/hazard group relativity adjusts for differences in claim size by location and business classification. For two risks with the same expected loss, if one of the risks is expected to have more severe individual losses then the relativity adjusts its expected loss downwards, which increases the volatility which is then reflected in a higher insurance charge and lower insurance savings.
Question: What do we assume when using a state/hazard group relativity with a Table M?
- Solution:
- We assume the state/hazard group in question has a severity distribution that is closely related to the severity distribution of the Table M used, i.e. the distributions only differ in scale.
mini BattleQuiz 3 You must be logged in or this will not work.
| Full BattleQuiz | Excel Files | Forum |
You must be logged in or this will not work.
Pop Quiz Answers
To prove the relationship it is helpful to observe the area under F(y) equals 1 so [math]T+W+U+X=1[/math]. Similarly, the entry ratio r creates a rectangle of area r so [math]r=S+T+U[/math]. Then [math]\begin{align}\phi_D^\star(r) +r-1 &= (X+T+W) +(S+T+U) - (T+W+X+U) \\ &= S+T \\ &= \psi_D^\star(r).\end{align}[/math]